Introduction to Logic

Introduction to Logic#

some intro to the intro …

Big Ideas of Logic:

  • Validity

  • Formal Language

  • Decidability

  • Satisfiability

  • Duality between Syntax and Semantics

  • Proof Theory

  • Model Theory

  • Soundness and Completenss

  • Incompleteness

Validity#

An important idea often attributed to Aristotle is the following: To check whether an argument is valid, one does not need to understand its content. This surprising insight is at the heart of artificial intelligence.

The classic example is:

All men are mortal.
Socrates is a man.
Therefore, Socrates is mortal.

Clearly, this is a valid argument … but how do we know that it is valid?

We know that it is valid because of its form, not because we know anything about Socrates, men, or mortality. The form is:

All X are Y.
Z is an X.
Therefore, Z is Y.

This pattern holds regardless of what X, Y, and Z represent. We can substitute:

  • X = “programming languages”, Y = “formal systems”, Z = “Dafny”

  • X = “cities”, Y = “locations”, Z = “Paris”

The argument remains valid in all cases. This is the power of formal reasoning: validity depends only on the structure of the argument, not its content.

Formal Language#

Mathematically, a formal language is the smallest set closed under a finite number rules. Some examples:

  • The natural numbers are the smallest set containing “zero” and closed under “plus one”.

  • A programming language is the set of strings (or abstract syntax trees) that can be derived by the context-free grammar of the language, a classic example being the grammar of the C language and we will see later the grammar of Promela in Chapter 7: Temporal Logic with Spin.

  • The language of propositional logic is the smallest set containing a given set of atomic propositions (strings) and being closed under the operations AND (\(\wedge\)), OR (\(\vee\)), NOT (\(\neg\)).

Formal languages can be processed by algorithms. In particular, for any given formal language there are (terminating, even efficient) algorithms that

  • answer the yes-no-question, for any string, whether that string belongs to the language,

  • parse a given string into an abstract syntax tree.

Decidability#

Some logical questions are decidable: There exists an algorithm that, for any input, will eventually halt and give a correct yes-or-no answer. For example, in Chapters 2, 4, 5, 7, 8 we will meet software tools based on algorithms that decide the satisfiability problem of various logics.

Other questions are undecidable: No algorithm exists that can always provide an answer. Famously, Turing’s Halting Problem shows that there is no algorithm that can decide, for any program, whether that program terminates on all inputs.

Satisfiability#

We remember from school various techniques to solve algebraic equations, maybe most famously the formula for the solutions of the quadratic equation. After Aristotle, the next important progress in logic was by George Boole who in his groundbreaking work Mathematical Analysis of Logic (I recommend to read at least the introduction) introduced the idea that we can calculate with logic (and probability) in much the same way we calculate with real numbers in algebra and the infinitesimal calculus.

Maybe this can nowadays best be explained with the help of Sudoku. To focus on the main idea let us look at a 2x2 Sudoku:

\[\begin{split} \begin{array}{|c|c|} \hline 1 & {\ \ } \\ \hline & \\ \hline \end{array} \end{split}\]

which has the solution

\[\begin{split} \begin{array}{|c|c|} \hline 1 & 2 \\ \hline 2 & 1 \\ \hline \end{array} \end{split}\]

We can encode this puzzle using Boolean logic as follows. Let us label the four cells as p, q, r, s:

\[\begin{split} \begin{array}{|c|c|} \hline p & q \\ \hline r & s \\ \hline \end{array} \end{split}\]

The variables \(p, q, r, s\) are bits taking values in \(\{0,1\}\).

The intended encoding is as follows. For each cell, let’s say the bit is 1 when the cell contains 1, and 0 when it contains 2. In the notation of propositional logic of Chapters 1 and 2, a specification of the puzzle can now be expressed as follows.

First, the rules of Sudoku are transformed into the following equations (writing \(\vee\) for OR and \(\neg\) for NOT)

\[\begin{split} \begin{align*} (p \vee q) &= 1 &\text{first row contains a 1} \\ (\neg p \vee \neg q) &= 1 &\text{first row contains a 2} \\ (p \vee r) &= 1 &\text{first column contains a 1} \\ (\neg p \vee \neg r) &= 1 &\text{first column contains a 2} \\ (q \vee s) &= 1 &\text{second column contains a 1} \\ (\neg q \vee \neg s) &= 1 &\text{second column contains a 2} \\ (r \vee s) &= 1 &\text{second row contains a 1} \\ (\neg r \vee \neg s) &= 1 &\text{second row contains a 2} \end{align*} \end{split}\]

Second, the particular starting position is encoded by

\[ \begin{align*} p&= 1 &\text{upper left corner is 1} \end{align*} \]

Now we encoded the puzzle

\[\begin{split} \begin{array}{|c|c|} \hline 1 & {\ \ } \\ \hline & \\ \hline \end{array} \end{split}\]

as a formula in propositional logic finding a solution to the puzzle is the same as finding an assignment of truth values for the variables satisfying the logical specification of the puzzle.

The software tools of Chapters 2, 4, 5, 7, 8 are all elaborations of this simple idea of algorithms solving logical equations.

Remark: Satisfiability solvers are now used everywhere in software engineering, very much like numerical methods in more traditional areas of engineering. This is a fairly recent development: Only since the beginning of the 21st century, Boole’s 1847 vision of “a Calculus of Deductive Reasoning” has become mainstream engineering on a par with Newton’s and Leibniz’s infinitesimal calculus.

Duality between Syntax and Semantics#

Satisfiability is a relation between models (semantics) and formulas (syntax). This relation is commonly written in symbolic notation as

\[ M\models\phi \]

where \(M\) denotes a model and \(\phi\) (“phi”) a formula. \(M\models\phi\) is read as “\(M\) satisfies \(\phi\)” or “\(\phi\) is true in \(M\)” or “\(\phi\) holds in \(M\)”. In terms of the Sudoku example, \(\phi\) is the specification representing the rules of the game together with a particular starting position and \(M\) is the solution (satisfying assignment).

The reason that this is called a duality is that adding more equations means specifying fewer solutions.

With a little mathematics, we can see that such a duality is a rather general phenomenon. For any relation \(R\subseteq X\times A\), there are functions

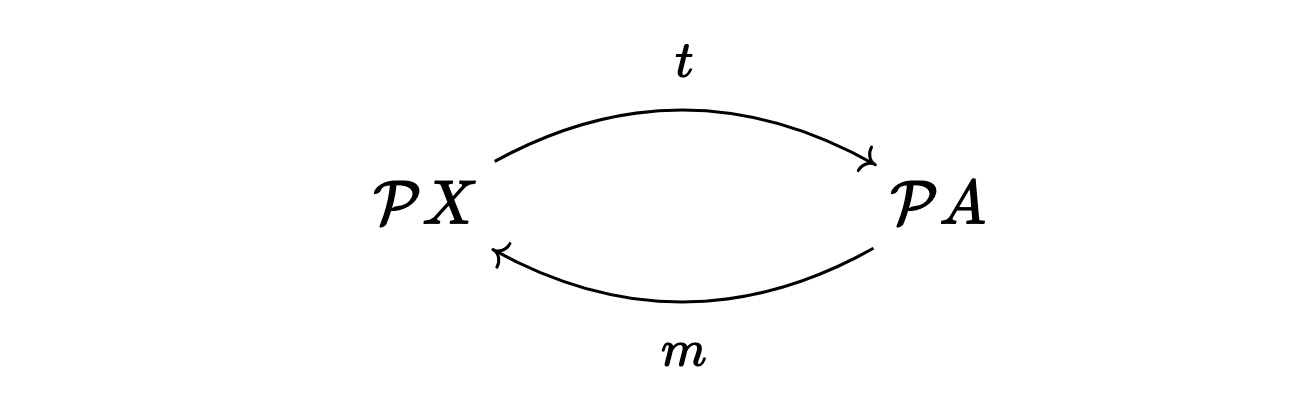
../_images/2025-10-26-14-31-31.png

between the set \(\mathcal PX\) of subsets of \(X\) and the set \(\mathcal PA\) of subsets of \(A\) defined by [1]

\[\begin{split} \begin{gather*} t(S)=\{a\in A\mid xRa \text{ for all } x\in S\}\\ m(T)=\{x\in X\mid xRa \text{ for all } a\in T\}\\ \end{gather*} \end{split}\]

In the example of satisfiability, we read this as follows:

  • \(t(S)\) is the largest theory satisfied by all models in \(S\).

  • \(m(T)\) is the set of all solutions specified by the theory \(T\).

Proof Theory#

…

Model Theory#

…

Soundness and Completenss#

…

Incompleteness#

…

Contents